- 징검다리 건너기
[본 문제는 정확성과 효율성 테스트 각각 점수가 있는 문제입니다.]
카카오 초등학교의 "니니즈 친구들"이 "라이언" 선생님과 함께 가을 소풍을 가는 중에 징검다리가 있는 개울을 만나서 건너편으로 건너려고 합니다. "라이언" 선생님은 "니니즈 친구들"이 무사히 징검다리를 건널 수 있도록 다음과 같이 규칙을 만들었습니다.
- 징검다리는 일렬로 놓여 있고 각 징검다리의 디딤돌에는 모두 숫자가 적혀 있으며 디딤돌의 숫자는 한 번 밟을 때마다 1씩 줄어듭니다.
- 디딤돌의 숫자가 0이 되면 더 이상 밟을 수 없으며 이때는 그 다음 디딤돌로 한번에 여러 칸을 건너 뛸 수 있습니다.
- 단, 다음으로 밟을 수 있는 디딤돌이 여러 개인 경우 무조건 가장 가까운 디딤돌로만 건너뛸 수 있습니다.
"니니즈 친구들"은 개울의 왼쪽에 있으며, 개울의 오른쪽 건너편에 도착해야 징검다리를 건넌 것으로 인정합니다.
"니니즈 친구들"은 한 번에 한 명씩 징검다리를 건너야 하며, 한 친구가 징검다리를 모두 건넌 후에 그 다음 친구가 건너기 시작합니다.
디딤돌에 적힌 숫자가 순서대로 담긴 배열 stones와 한 번에 건너뛸 수 있는 디딤돌의 최대 칸수 k가 매개변수로 주어질 때, 최대 몇 명까지 징검다리를 건널 수 있는지 return 하도록 solution 함수를 완성해주세요.
[제한사항]
- 징검다리를 건너야 하는 니니즈 친구들의 수는 무제한 이라고 간주합니다.
- stones 배열의 크기는 1 이상 200,000 이하입니다.
- stones 배열 각 원소들의 값은 1 이상 200,000,000 이하인 자연수입니다.
- k는 1 이상 stones의 길이 이하인 자연수입니다.
[입출력 예]stoneskresult
| [2, 4, 5, 3, 2, 1, 4, 2, 5, 1] | 3 | 3 |
입출력 예 #1
첫 번째 친구는 다음과 같이 징검다리를 건널 수 있습니다.
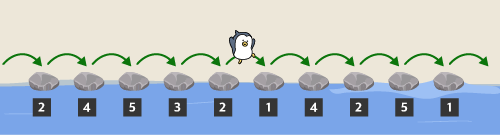
첫 번째 친구가 징검다리를 건넌 후 디딤돌에 적힌 숫자는 아래 그림과 같습니다.
두 번째 친구도 아래 그림과 같이 징검다리를 건널 수 있습니다.
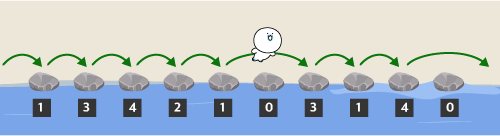
두 번째 친구가 징검다리를 건넌 후 디딤돌에 적힌 숫자는 아래 그림과 같습니다.
세 번째 친구도 아래 그림과 같이 징검다리를 건널 수 있습니다.

세 번째 친구가 징검다리를 건넌 후 디딤돌에 적힌 숫자는 아래 그림과 같습니다.
네 번째 친구가 징검다리를 건너려면, 세 번째 디딤돌에서 일곱 번째 디딤돌로 네 칸을 건너뛰어야 합니다. 하지만 k = 3 이므로 건너뛸 수 없습니다.

따라서 최대 3명이 디딤돌을 모두 건널 수 있습니다.
풀이과정
1. 이 문제는 배열 요소 하나하나에 접근해서 탐색할 경우 최대 200.000 X 200.000.000 경우의 수가 나옵니다. 따라서 경우의 수가 터무니없이 나오기 때문에 이분 탐색을 이용하여 문제를 해결했습니다.
2. 이분탐색을 이용하기 위해 시작 지점과 끝 지점을 선언하였습니다. 끝 지점 같은 경우 값의 최대로 해도 되지만 경우의 수를 줄이기 위해 배열에서 가장 큰 값을 선택했습니다.
3. 탐색을 하면서 그 수를 통해 강을 건널 수 있는지 판단을 하며 탐색 범위를 좁혀 나갑니다.
건널 수 있을 경우 : ( mid + 1 ) 건널 수 없을 경우 : ( mid - 1 )
4. 탐색이 끝나면 start의 값을 반환합니다.
코드
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int K;
bool isgo(int n ,vector<int> &stones)
{
int count = 0;
for(int i = 0; i < stones.size(); i++)
{
if(stones[i] - n <= 0)
count++;
else
count = 0;
if(count >= K)
return true;
}
return false;
}
int solution(vector<int> stones, int k) {
int answer = 0;
K = k;
int start = 0, end = *max_element(stones.begin(),stones.end());
int mid;
while(start <= end)
{
mid = ( start + end ) / 2;
if (isgo(mid,stones))
{
end = mid - 1;
}
else
{
start = mid + 1;
}
}
return start;
}
